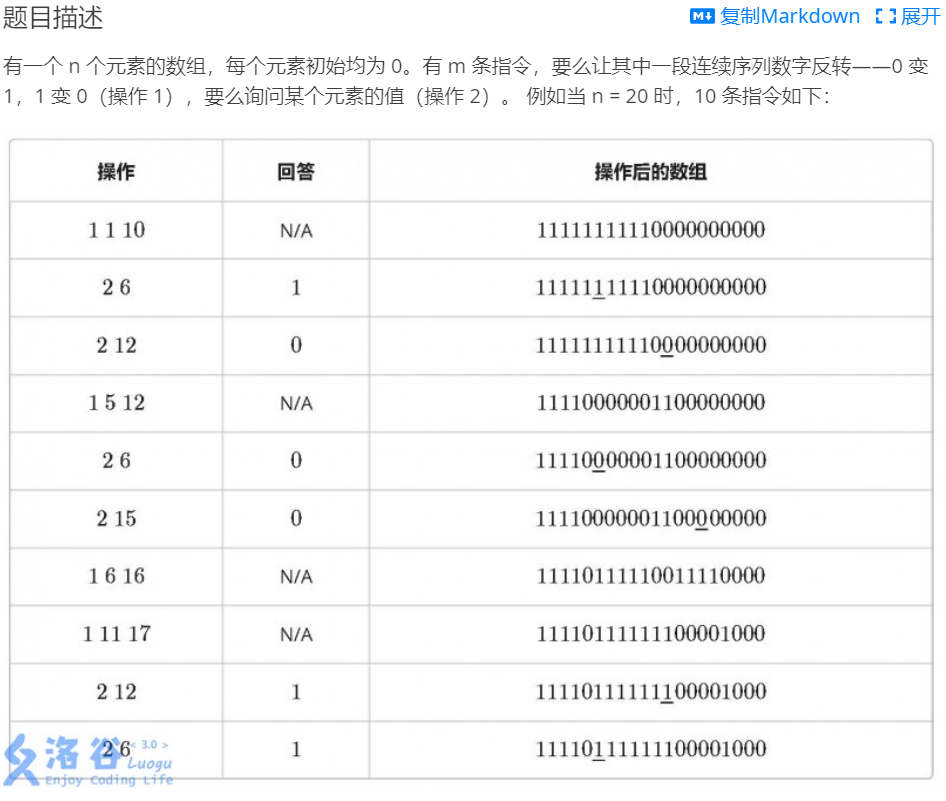
树状数组进阶练习

发表于 2022/09/03

作者 Dignite

・・ 11 分钟阅读

通过这些练习，我们能对树状数组有更深刻的理解。这里给题目排的顺序是难度不严格递增的。

P4939 Agent2

这道题是典型的树状数组+差分。我们在开始咕的天数打上标记 $+1$ ，结束咕的那天的后一天打上标记 $-1$ ，那么这段天数就代表了多了一个咕咕咕。

P5057 [CQOI2006]简单题

这题同样也是树状数组的标签。注意，树状数组能处理的是和前缀有关的问题。不论是前缀和，还是这道题的前缀布尔。这道题仍然是差分的思想，但我们需要抽象成布尔，即让每一个数字都是由一些真/假的与运算得来的。为什么用与？因为对于任意一个布尔值，我再与一个真/假，最后的结果可以由我决定；如果用或，如果已经是真了，不管再或一个真假还是真。当然，异或理论上也是可行的。

我们可以在树状数组+差分代码的基础上稍加修改：

void change(int x){
    while(x<=n){
        bit[x]=!bit[x];
        x+=lowbit(x);
    }
}
bool query(int x){
    bool ans=0;
    while(x>0){//边界条件x>0!
        if(bit[x]){
            ans=!ans;
        }
        x-=lowbit(x);
    }
    return ans;
}

P5094 [USACO04OPEN] MooFest G 加强版

我们来看样例：

位置: 1 2 3 4 5 6
听力: 3   4   2 2

首先当然不能 $O(n^2)$ 地去求答案，第一步我们要想出一种办法能有序地求出答案。让我们对奶牛按听力进行从小到大排序，那么对于一个当前选出的奶牛来说，之前的奶牛的听力肯定比当前的小，所以它是目前听力最大的。这个时候，我们只需将这个奶牛的听力去乘上所有的位置之差即可。

我们根据这个想法，看样例列出以下算式：

2*(6-5)+3*((5-1)+(6-1))+4*((6-3)+(5-3)+(3-1))=57=样例输出

现在我们来处理每个加式的乘号后面的内容。我们注意到，对于位置在当前奶牛之前的，这个位置之差应当是当前的减去前面的；反之亦然。进一步展开，我们发现所有位置在当前奶牛之前的位置之差应当是前面的位置之和减去当前奶牛位置乘以前面奶牛的个数；反之亦然。所以我们需要维护的是位置比当前奶牛小的奶牛的位置值之和，以及位置比当前奶牛小的奶牛的个数。

这样只维护了位置比当前奶牛小的。大的呢需要再另外维护两个吗？我们可以把所有奶牛的位置加起来，个数加起来，这样总数减去前面的就是后面的了。

for(int i=1;i<=n;i++){
    sum+=a[i].x;
    change(a[i].x,1);
    change2(a[i].x,a[i].x);
    if(i==1){
        continue;
    }
    int xiao_geshu=query(a[i].x-1); // 小的个数
    int da_geshu=i-xiao_geshu-1;
    int xiao_zhihe=query2(a[i].x-1); // 小的之和
    int da_zhihe=sum-a[i].x-xiao_zhihe;
    ans+=a[i].v*(da_zhihe-da_geshu*a[i].x+xiao_geshu*a[i].x-xiao_zhihe);
    }

P1637 三元上升子序列

之前做过一个求字符串中子序列 gao 的个数。这题的其中一个思路是对于每一个 a ，向前向后看 g 和 o 的个数，然后乘起来，再累加。

而本题的思路也是相类似的。我们对于原数列中每一个数，将其前面比当前数字小的个数乘上后面比当前数字大的个数，然后再累加。遍历原数列中每个数是 $O(n)$ 的，我们要再用 $O(logn)$ 的复杂度求出前后的数字个数。

for(int i=1;i<=n;i++){
	change(a[i],1);
	if(i==1||i==n)continue;
	l[i]=query(a[i]-1);
}
init();
for(int i=n;i>=1;i--){
	change(maxn-a[i],1);
	if(i==1||i==n)continue;
	r[i]=query(maxn-a[i]-1);
}

P3431 [POI2005]AUT-The Bus

对于这类题，首先考虑使用 dp 。令 dp[i] 表示看到第 i 个点，所能接到的乘客的最大值。显然， dp[i]=max{dp[k]，其中点k的在点i的左上角} 。注意数据范围： $1\le n\le 10^9$, $1\le m\le 10^9$, $1\le k\le 10^5$ 。我们首先要给坐标离散化，然后对于每一个点找出它左上角点的最大值。

看到最大值，我们又可以对树状数组进行改造了。

void update(int x,int y){
	while(x<maxn-5){
		bit[x]=max(bit[x],y);
//		bit[x]+=y;
		x+=lowbit(x);
	}
}
int query(int x){
	int ans=0;
	while(x>0){
//		ans+=bit[x];
		ans=max(ans,bit[x]);
		x-=lowbit(x);
	}
	return ans;
}

要想求出一个 $dp[i]$ ，我们必须先求好所有横坐标、纵坐标都小于等于当前点的，那么让我们先把纵坐标从小到大排序，再横坐标从小到大排序。对于每一个纵坐标，遍历从左到右的横坐标。其上方的点肯定是更新过了，左边的点也更新过了。更新的时候把横坐标更新成当前算出来的 $dp$ 值即可。

P2448 无尽的生命

这道题细节比较多，~~也比较毒瘤~~，首先要给输入离散化，完了以后把没有要求要交换空区间合并起来，然后再按逆序对做。~~是不是很简单？~~

事实上是我太菜了。

P3253 [JLOI2013]删除物品

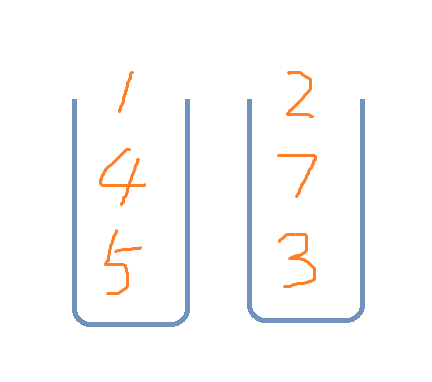
讲的是把两个栈里的东西翻来倒去的逝情。我们简化一下题意。原来的两个栈是这样的：

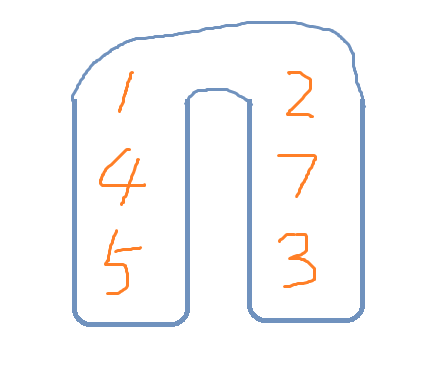
想象一下把一个元素搞到另一个栈的栈顶的操作。我们把它演化成下面这样：

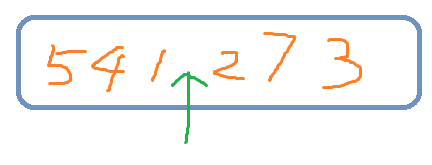
没错，就是把两个栈顶连起来。再把它拉直：

就像这样。其中，绿色的箭头标注了原来栈顶的位置。想要把一个元素放到另一个栈里，相当于就是改变了栈顶的位置，即移动绿色的箭头。

我们很容易把输入数据弄成这样一个数列。我们让这个绿色的箭头 $ptr$ 表示 $a[ptr]$ 与 $a[ptr+1]$ 这两个元素在栈顶。我们每次要找到最大的那个数的位置，就要考虑如何求出移动的步数。因为数字是不重复的，所以我们记录每一个数字的下标，然后在树状数组中该下标加上 $1$ ，就代表此处有一个数字。那么显然要移动的步数就是两个数字间的数字个数，可以用树状数组处理。当删除了一个数字，就在当前位置减去 $1$ ，表示当前数字被删除了。

注意这道题也需要离散化。

P3531 [POI2012]LIT-Letters

我们来考虑什么情况下交换次数最少。首先，如果字符串没有重复的字母，显然最少交换次数就类似于冒泡排序，一个一个相邻的排过去。如果有重复的字母，应该要让原来在前的，最后也在前。这恰好类似于一个稳定的冒泡排序。

然后我们怎样快速求出要交换的次数呢？事实上，对于一个本来就上升的数列，如 1, 2, 3, 4, 5 ，如果把其中任意一个数往前移一个，如变成了 1 , 3, 2 ,4 ,5 ，就会多出一个逆序对；再移一次，又多出一个，总共两个。以上是一个正确的结论，且对于任意一个数列（不论顺序是上升、下降还是乱序），只要移了一个，就会多出一个逆序对。

所以这道题我们也是求逆序对的个数就可以了。