树状数组自学笔记

1 树状数组能解决什么问题？

先看例题 P3374 【模板】树状数组 1 。对于一个数列，我们需要支持以下两个操作：

1. 将某一个数加上 $x$ ；
2. 求出某区间每一个数的和。

对于这道题，如果用普通的方法暴力枚举，我们可能只会拿到70%的分数。然而如果利用树状数组，我们就能获得满分。可见：树状数组能够支持动态修改并查询前缀和，从而求出某区间的和。

2 树状数组的结构是怎样的？

我们直接来5个点（点中的数字是编号，不是值）。

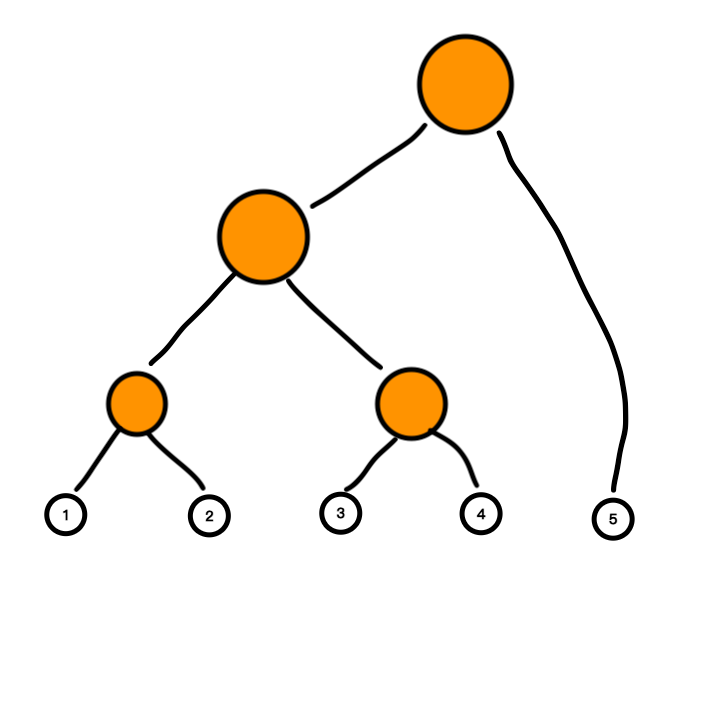
接下来，让我们建立一棵树。

以每两个节点作为叶子结点向上建立二叉树。

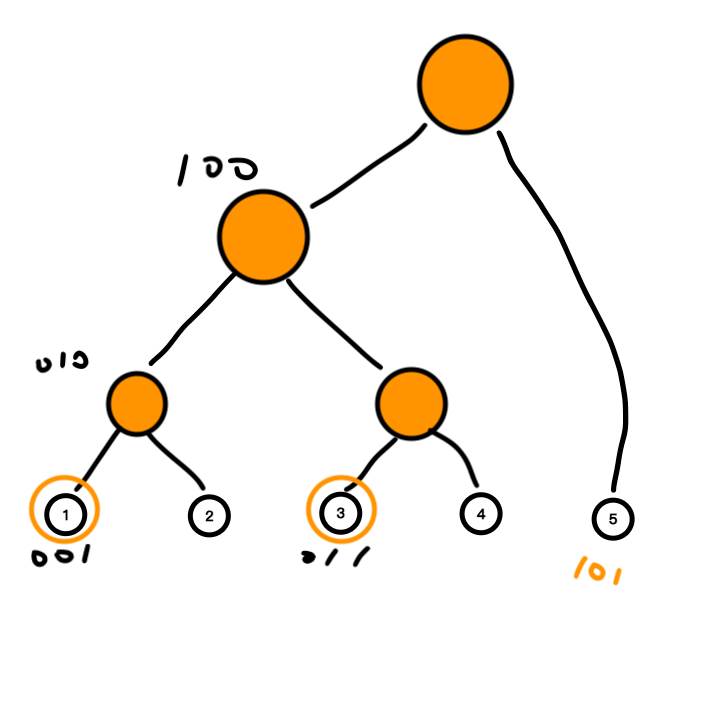
每一个橙色的节点就表示其所有字树的和。下面让我们为橙色节点也标上编号。特别地，对于节点1, 3 和 5，我们把它标记为特殊的橙色节点（原因以及标法下面会讲）。节点编号用二进制表示。

我们先约定，对于原数组，我们用数组 $a$ 来储存；而橙色节点的数组我们用 $bit$ 来储存（注意，有些并不是所有橙色节点都有编号。对于没有编号的橙色节点，我们就不用管它了）。

下面我们列出一些等式关系：

• $bit[001] = a[001]$
• $bit[010] = a[001] + a[010]$
• $bit[011] = a[011]$
• $bit[100] = a[001] + a[010] + a[011] + a[100]$
• $bit[101] = a[001] + a[010] + a[011] + a[100] + a[101]$

很难发现规律？我们换个角度看。

• 对于 $a[001]$，它被包含在 $bit[010], bit[100]$ 中；
• 对于 $a[010]$，它被包含在 $bit[010], bit[100]$ 中；
• 对于 $a[011]$，它被包含在 $bit[100]$ 中；
• 对于 $a[101]$，它被包含在 $bit[101]$ 中。

如果把树画得大一点，可能会更容易地发现规律。而规律就是：对于任意一个 $a[x]$，每次取 $x$ 的最低位并加上 $x$，就能一步一步地找到它所有的父亲。

是不是很神奇？我们拿 $a[001]$ 来举个例子，加深理解。

1. 首先，$a[001]$ 的第一个父亲为 $001$ 本身，是 $bit[001]$；
2. 取到 $001$ 的最低位的值 $001$，$001 + 001 = 010$，那么$bit[010]$ 就是它的第二个父亲。
3. 再然后，$010 + 010 = 100$，则 $bit[100]$ 就是第三个父亲。

3 用代码实现单点修改

了解了基本的树状数组的构造方式，让我们来实现原数组的单点修改。

我们知道，$bit$ 数组存的是它下面所有孩子的和；相反地，若要修改一个 $a$ 的值，就要修改它每一个父亲的值。而这就要用到上一章节中提到的如何遍历每一个父亲的方法。

3.1 怎样获得最小一位二进制的值？

先给出结论：x & - x。这需要用到反码补码的知识。

首先，$x$ 是一个二进制正整数。那么，$- x$ 的原码就是把最高位的0变成了1，其反码就是最高位的1不变，剩下的所有数位取反。$- x$ 的补码就是在反码的基础上加1。而 $x$ 的补码与原码相同。那么，两者取与，最高位一个是1一个是0，变成了0；剩下的数位，假设 $x$ 的原码最低位是1，那么 $x$ 的补码最低位就是1，而 $- x$ 的补码的最低位是0+1=1，而其他数位都恰好相反，所以前面的全部是0，只有最低位为1。类似地，如果最低位不是1，那么负数的反码加上1后只有最低的那位会进位，使得只有这位和正数的补码与上后会变成1，其它都是0。

于是我们定义函数 lowbit：

int lowbit(int x){
	return x & -x;
} 

它的作用是返回最低位的1的值。

3.2 实现遍历所有父亲节点并加上一个值

1. 首先，$a[x]$ 的第一个父亲节点就是 $bit[x]$，这就是起点。
2. 然后，我们将 $x$ 每次加上 $lowbit(x)$ （注意：lowbit(x)中的x是不断更新的x，而不是最开始的不变的x）x += lowbit(x); 。
3. 对于每一个访问到的节点，都加上一个值 $y$ bit[x] += y; 。
4. 边界条件：当父亲节点编号 $x > n$ 时（节点最多n个），退出循环 while(x <= n) 。

于是得到函数 change：

void change(int x, int y){
	while(x <= n){
		bit[x] += y;
		x += lowbit(x);
	}
}

change函数能将所有包含 x 的父亲加上 y。

OK，现在我们实现了第一个任务：动态修改区间和。下面我们要实现动态查询区间和。

4 查询区间和

现在，给出任意的两个端点 $[ l , r ]$，要求出 $a[ l ] + … + a[ r ]$，应该怎么做呢？

回想普通前缀和的做法，我们只要求出 $pre[ r ] - pre[ l - 1 ]$ 即可。类似地，我们要利用树状数组求出区间和，就要写一个 query （查询）函数，来求出 $a[1] + … + a[n]$ 的值，相当于普通前缀和中 pre 的功效，从而就能轻松求出某一区间的和了。

4.1 实现 query 函数

之前我们说过，要修改单点的值，就要遍历所有父亲，用的方法是 x += lowbit(x);。那如果是获取 $a[1] + … + a[n]$ 的值，是否也能用类似的方法呢？让我们把之前的图搬出来再来找找规律。

假设我们现在要获取 $a[1] + a[2] + a[3]$ 的值。此时 $n = 011$ ，则 $n - lowbit(n) = 010$（既然修改时是加上lowbit，那么查询时就反一下，减去lowbit），恰好能得到 $a[1] + a[2]$ 的和。如此一来，我们就能求出 $1 ~ n$ 的区间和了。

int query(int x){
	int res = 0;
	while(x){
		res += bit[x];
		x -= lowbit(x);
	}
	return res;
}

注意边界条件：x应该大于0。

4.2 求出区间和

之前说过，query 就相当于 pre，所以易得：

query(r) - query(l - 1)

这就是区间 $[l , r]$ 的值了。

5 示例代码

#include<cstdio>
#include<iostream>
using namespace std;
const int maxn=5e5+10;
int n,m;
int a[maxn];
int bit[maxn];
int k,x,y;
int lowbit(int x){
    return x & -x;
}
void change(int x,int y){
    while(x<=n){
        bit[x]+=y;
        x+=lowbit(x);
    }
}
int query(int x){
    int ans=0;
    while(x>0){//边界条件x>0!
        ans+=bit[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        change(i,a[i]);//一开始都是0，要初始化加上a[i]
    }
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&k,&x,&y);
        if(k==1){
            change(x,y);//将第x个数加上y
        }else{
            printf("%d\n",query(y)-query(x-1));//求出区间和
        }
    }
    return 0;
}

注意：请使用较快的输入输出，否则可能会超时。

6 FAQ

1. 为什么数组名称要叫做 bit ？ 答：因为树状数组的英文全称叫做 Binary Indexed Tree，简称 BIT。
2. 树状数组的时间复杂度是多少？ 答：虽然树状数组和线段树的理论时间复杂度都是 $O(log_2 n)$，但是树状数组代码简单，实际时间复杂度会略低一些。
3. 为什么能想到树状数组这样的数据结构？ 答：天才发明的，天知道。