从树状数组到线段树

从三味书屋到百草园（误）

1 树状数组回顾

1.1 lowbit 原理

众所周知，lowbit 取的是一个二进制数的最低位的数值，代码如下：

int lowbit(int x){
	return x&-x;
}

那么，为什么 x&-x 就能取到最低位呢？

我们来考虑一个二进制正数。由于我们取的是最低位，那么只需关注最低位的 $1$ 即可。下面让我们来大致描述一下这个数：

\[0101001 \cdots 010000\]

注意，这个数的第一位一定是 $0$ ，因为是个正数。而我们关注的是最后一个 $1$ ，所以只需观察它及其右边的 $0$ 即可。我们考虑这个数的补码，由于这个数是正数，所以补码等于原码，所以 lowbit 函数中 & 的左边就是这个数。

那么 $-x$ 又是多少呢？对于原码来说，两者的绝对值相同，只是符号位相反，所以 $-x$ 的原码就是把原来那个数的第一位 $0$ 改成 $1$ 。再考虑它的反码，就是除了符号位以外其它位全部取反。我们来看看它的反码：

\[1010110 \cdots 101111\]

注意看，将这个数加上 $1$ ，也就是成为了补码。你会得到：

\[1010110 \cdots 110000\]

因为反码的后面一串全是 $1$ ，所以我们加上了 $1$ 后后面的 $1$ 全部进位，就进到了原码是 $1$ 的位置，使后面的一串和正数的原码一样。而其余的位都不一样，进行与运算后，都变成了 $0$ ，就留下了 $1$ 这一位。大功告成。

1.2 树状数组概念澄清

在树状数组中有这么一些概念：

1. 原数组（ $a$ 数组）
2. $bit$ 数组
3. $add$ 函数
4. $query$ 函数

任何的研究都应该从宏观到微观，所以我们研究树状数组也是先看使用对象再看实现过程。 ——鲁迅

现在我们的目标是求出一个原数组的区间和（或者说前缀和也行），并且还能支持单点修改原数组。注意，这里的原数组不管是什么东西，普通数组也好，差分数组也好，我们维护的是数组本身的前缀和，而不关心原数组是做什么的。

$add$ 函数能够标记维护的数组中某个数值的改变， $query$ 函数能够查询维护数组的前缀和。

这样一来，我们就对树状数组有了更深刻的理解。让我们来看看下面这一题。

1.3 区间修改，单点查询

如题，已知一个数列，你需要进行下面两种操作： 将某区间每一个数加上 x ； 求出某一个数的值。 —— 洛谷 P3368

说到给某个区间全部加上一个数，我们很容易想到差分。在差分数组中，我们给差分数组的起始位置和末位置打标记，对于原数组，就是求差分数组的前缀和。

我们来看以上思路的两个关键点：

1. 给差分数组的某些位置打上标记，也就是改变数值；
2. 求差分数组的前缀和。

我们再来看上面刚刚说过的话：

$add$ 函数能够标记维护的数组中某个数值的改变， $query$ 函数能够查询维护数组的前缀和。

所以想到什么了吗？我们可以用树状数组维护差分数组，并单点修改差分数组，查询差分数组前缀和。而这个前缀和恰好就是题目中要求的某个数。所以代码就出来了。

基本代码还是一样，改一下两点：

1. 在读入的时候，初始数组要分配到差分数组里，所以要进行如下操作：

   for(int i=1;i<=n;i++){
    cin>>a[i];
    add(i,a[i]);
    add(i+1,-a[i]);
   }
   

2. 修改与查询操作，按照上面的思路即可：

   for(int i=1;i<=m;i++){
    cin>>cmd;
    if(cmd==1){
        cin>>x>>y>>k;
        add(x,k);
        add(y+1,-k);
    }else{
        cin>>x;
        cout<<query(x)<<endl;
    }
   }
   

1.4 区间修改，区间查询

太复杂了，如果不用线段树，用树状数组怎么做呢？

如题，已知一个数列，你需要进行下面两种操作： 将某区间每一个数加上 kk。 求出某区间每一个数的和。 —— 洛谷 P3372

1.4.1 推导

推公式时间到！我们沿用上一题差分数组的思想。

假设 $a$ 是原数组， $b$ 是差分数组。那么易知：

\[a[x]=\sum_{i=1}^{x}b[i]\]

对于一个 $a$ 数组的前缀和，我们得到：

\[\sum_{x=1}^{n}a[x] = \sum_{i=1}^{x} \sum_{j=1}^{i} b[j]\]

展开，得到

\[\sum_{x=1}^{n} a[x] = \sum_{i=1}^{x} (x-i-1) \times b[i]\]

进行常变分离，得到：

\[\sum_{x=1}^{n}a[x] = \sum_{i=1}^{x} (x-1) \times b[i] - \sum_{i=1}^{x} i \times b[i]\]

公式推导完毕。我们发现 $a$ 数组的前缀和与 $(x-1) \times b[i]$ 有关，与 $ i \times b[i]$ 也有关。前面一个还好说，维护一个 $b$ 数组的树状数组，求出其前缀和，在输出答案的时候乘上一个查询的 $x$ 减去 $1$ 即可。而 $ i \times b[i]$ 有 $i$ 又有 $b[i]$ ，它的前缀和该如何维护呢？

陷入了思维困境。我们来仔细考虑一下，树状数组做的是什么？维护数组前缀和。那么 $ i \times b[i]$ 不是数组怎么办？注意，对于任意的 $i$ ，$i$ 是确定的， $b[i]$ 也是确定的， $ i \times b[i]$ 就是确定的了！你一定假想 $i$ 和 $b[i]$ 并没有一一对应的关系，然而它们是唯一确定的。

这么说就好办了，我们让每一个 $ i \times b[i]$ 成为另外一个数组的每一个元素，再进行运算。 $bit1$ 用于维护 $b[1]+…+b[x]$ ， $bit2$ 用于维护 $i \times b[1]+(i-1) \times b[2]+…+1 \times b[i]$ 。

对于 $a$ 数组的前缀和，就是 $b$ 数组的前缀和乘上 $(x-1)$ 再减去 $i \times b[i]$ 数组的前缀和。

$b$ 是什么？ $b$ 是差分数组。所以我们仍然要对其进行差分的基本操作。只是存储的时候要在 $b$ 数组上加一点“花边”。

1.4.2 Code

#include <bits/stdc++.h>
#define int long long // 别忘了开 long long
using namespace std;
const int maxn=5e5+10;
int a[maxn];
int bit1[maxn];
int bit2[maxn];
int n,m;
int cmd,x,y,k;
int lowbit(int x){
    return x&-x;
}
void add1(int x,int y){
    while(x<=n){
        bit1[x]+=y;
        x+=lowbit(x);
    }
}
void add2(int x,int y){
    while(x<=n){
        bit2[x]+=y;
        x+=lowbit(x);
    }
}
int query1(int x){
    int ans=0;
    while(x>0){//边界条件x>0!
        ans+=bit1[x];
        x-=lowbit(x);
    }
    return ans;
}
int query2(int x){
    int ans=0;
    while(x>0){//边界条件x>0!
        ans+=bit2[x];
        x-=lowbit(x);
    }
    return ans;
}
signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        add1(i,a[i]);
        add1(i+1,-a[i]);
        add2(i,a[i]*i);
        add2(i+1,-a[i]*(i+1));
    }
    for(int i=1;i<=m;i++){
        cin>>cmd;
        if(cmd==1){
            cin>>x>>y>>k;
            add1(x,k);
            add1(y+1,-k);
            add2(x,k*x);
            add2(y+1,-k*(y+1));
        }else{
            cin>>x>>y;
            cout<<(query1(y)*(y+1)-query2(y))-(query1(x-1)*(x)-query2(x-1))<<endl;
        }
    }
    return 0;
}

这么来看，树状数组过于复杂，其思路晦涩难懂，拓展性差。这时候，线段树就登场了。

2 线段树入门

2.1 构造

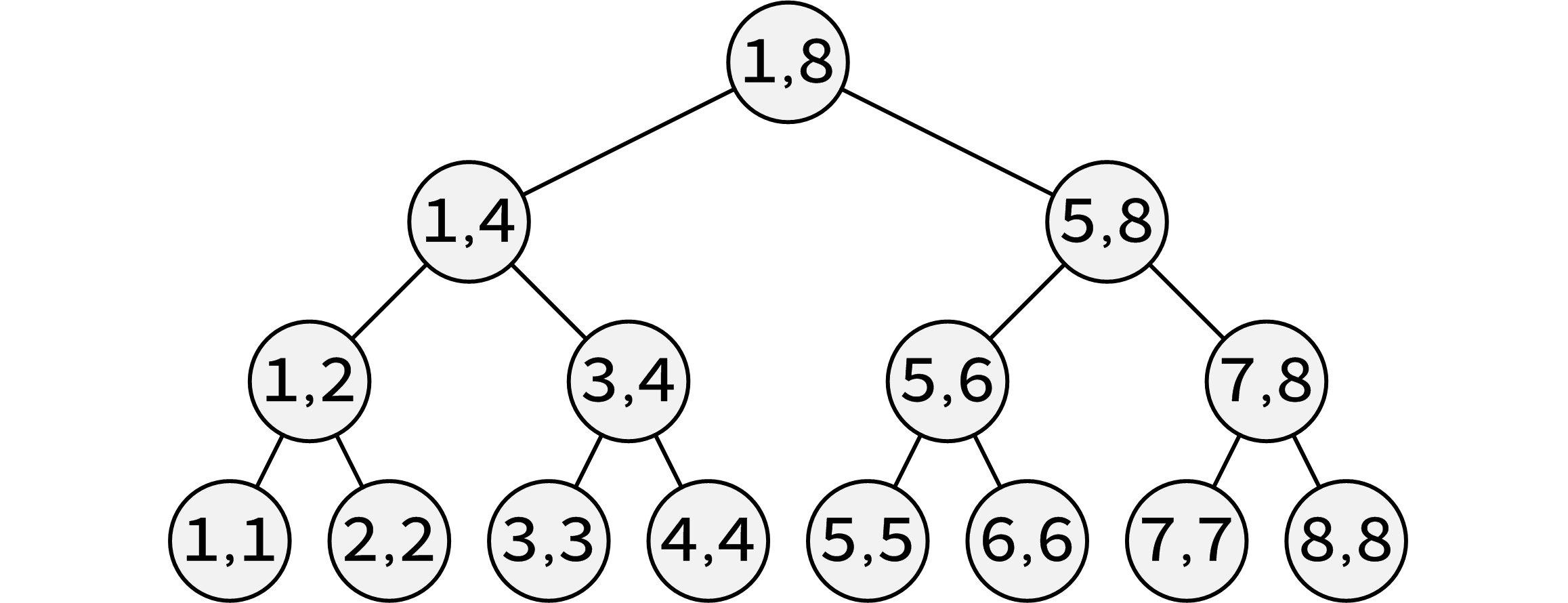
相较于树状数组，线段树没有复杂的二进制表示，而是使用了分治的思想，将一排数组一分为二，再一分为二，分成每一份都只有一个数字为止。如下图：

图片来自洛谷

其中，每一个节点逗号左右的两个数字表示了一个区间。最顶上的 $[1,8]$ 表示这个节点的值为原数组的 $a[1]+a[2]+…+a[8]$ 。同样，最底下的这些点如 $[1,1]$ 就只表示原数组的 $a[1]$ 。

下面我们来研究最基础的线段树：单点修改，区间查询。不考虑任何优化。

2.2 关于线段树的数组

如你所见，线段树是个二叉树。所以对于任意一个节点 $tree[x]$ ，我们用 $tree[x \times 2]$ 表示它的左儿子，用 $tree[x \times 2+1]$ 表示它的右儿子。其中，根节点的编号为 $1$ 。

那么这个数组要开多大呢？我们假设有原数组 $n$ 个元素。也就是线段树最后一排有 $n$ 个叶子节点（如图）。又由于这是一个满二叉树（当然很多情况下不会是满二叉树），所以它的节点总数大约是 $2 \times n$ 。但是，在编写代码时我们通常开 $4$ 倍的 $n$ ，甚至 $8$ 倍，别问我为什么。

2.3 初始化

下面是 init 函数！对于题目给出的原始数组，我们要把它存到线段树里面去。考虑一下，对于每一个数，这个数会影响到它头顶上哪些节点的值呢？当然是一路往上直到根节点上的所有节点都要修改。首先明确一点，在树上，我们用深度优先搜索。

我们定义 init(now,l,r) 表示当前在 $now$ 这个编号的节点，左边囊括到 $l$ ，右边延申到 $r$ 。那么当 $l=r$ 时，这个区间只有一个点了，那么就往回回溯，更新上面的点；如果 $l \neq r$ ，说明还没有到叶子节点，那么久将当前点区间一分为二，往下递归，递归完后再根据两个儿子更新自己的值。

void init(int now,int l,int r){
	if(l==r){
		tree[now]=a[now]; // a 是原数组
		return;
	}
	mid=l+r<<1; // 加号的优先级大于位运算！
	init(now*2,l,mid); // 左儿子
	init(now*2+1,mid+1,r); // 右儿子
	tree[now]=tree[now*2]+tree[now*2+1];
}

init(1,1,n);

2.4 单点更新操作

对于一个叶子节点加或减的更新，同样会影响到它头顶上一条路径的节点。但是我们是深度优先搜索，所以事实上的路径是从根节点寻找这个叶子节点的过程。对于每一个节点，我们都面临两条路的选择。而如何选择就成为了重点。

void update(int tar,int v,int s,int t,int p){
	// 我们要将原数组中 tar 这个位置加上 v ，
	// 也就是线段树 [tar,tar] 的节点加上 v 。
	// 当前的位置是节点 p，范围是 [s,t] 。
	tree[p]+=v;
	if(s==tar&&t==tar){
		return;
	}
	int mid=s+t<<1;
	if(tar<=mid){
		update(tar,v,s,mid,p*2);
	}else{
		update(tar,v,mid+1,t,p*2+1);
	}
}

2.5 区间查询操作

应该比较好理解，把一个大区间放到线段树顶端，然后一层一层切割，最后剩下来刚好线段树某一个节点的区间吻合的，就可以把答案加上去了。具体请看代码。

int query(int l,int r,int s,int t,int p){
	// [l,r] 表示要查询的目标区间，
	// [s,t] 表示当前所在的点所表示的区间，
	// p 是当前所在的点的编号。
	if(l<=s&&t<=r){
		// 说明当前区间包含于目标区间里了，就加上答案
		// 不要担心空余的区间会被遗漏，想一想当前这个区间是怎么达到的。
		return tree[p];
	}
	int mid=s+t<<1,ans=0;
	// 如果能走到这里，说明当前区间一定大于目标区间
	if(l<=mid){
		// 说明 [s,t] 的左边有一部分在 [l,r] 里
		ans+=query(l,r,s,mid,p*2);
	}
	if(mid<r){
		// 说明 [s,t] 的右边有一部分在 [l,r] 里
		ans+=query(l,r,mid+1,r,p*2+1);
	}
	return ans;
}