CF1693B Fake Plastic Trees 题解
中文题意
$t$ 组数据,每组给定一个 $n$ 个结点的树, 根为 $1$ ,给定 $2,3,\ldots ,n$ 的父结点 $p_2,p_3,\ldots ,p_n$ 。再给出每个点权值 $a_i$ 的范围 $[l_i,r_i]$ 。
初始每个点的权值均为 $0$ 。每次操作可以选择从 $1$ 开始的树上路径 $b_1,b_2,\ldots,b_k$ (不一定要在叶子处结束),将 $a_{b_i}$ 加上 $c_i$ ,其中 ${c_i}$ 是一个 非负单调非减 的 整数 数列。
问至少多少次操作,可以令所有点点权均在 $[l_i,r_i]$ 范围内。
从最简单的情况开始
我们把树简化成只有一条链,并且将每个点的最终范围也简化成一个定值。让我们根据这个情况造出以下样例:
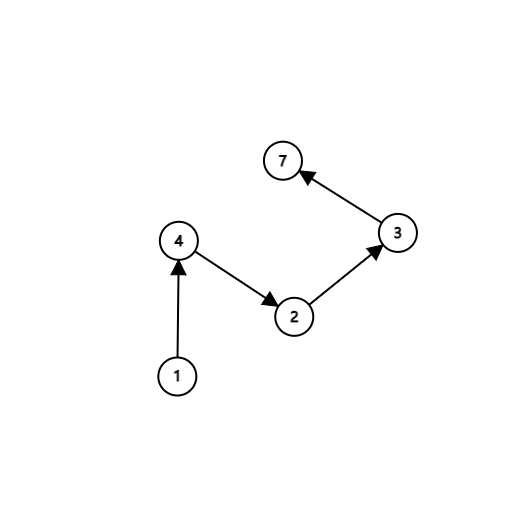
其中,根是1。题目要求我们从根开始到任意一点加上一个不严格递增的整数序列,显而易见,我们只需操作两次:
- 从根开始到
4,加上1, 4。 - 从根开始到
7,加上0, 0, 2, 3, 7。
由此可见,对于这种简单情况,最终操作的次数就取决于所谓的“瓶口”——后一个数小于前一个数的情况。因为我们的加上去的序列是连续递增的,所以当出现要求数字是递减时,就不得不让我们采取第二次行动。所以我们得出结论:操作次数等于链中后一个小于前一个的次数+1(这个1是最基本的操作次数,就是说即使这个链它全部直接是单调非减的,也要操作一次)。
如果是树呢?
现在更进一步,我们假设这个链表成为了一棵树,但是任然地,要求最终的答案还是一个定值。让我们在上面的样例中添上几根枝条。
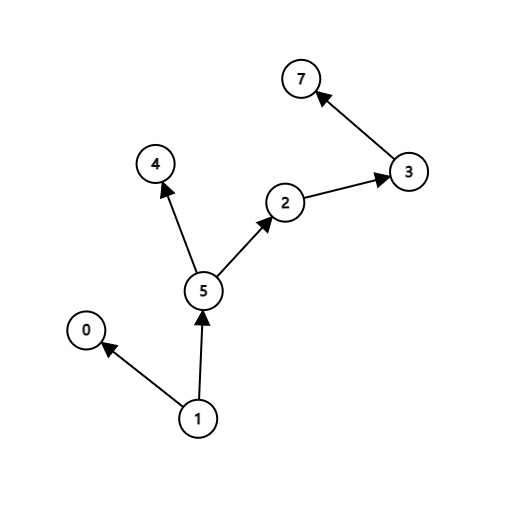
想一想:在这种情况下,什么时候要使操作次数加一呢?
首先我们先确定,对于每一个叶子节点,都要至少操作一次,即上面所说的“基本地”加一。但是,对于任意一个有孩子的节点来说,如何确定其操作次数呢?让我们来观察下面两个不同的例子:
例1
在这棵树中,显然我们操作两次就够了,因为对于每一条枝,我们假设最差情况,让根和孩子都加上相同的孩子的值,这样孩子成为了理想数值,根能大于等于其理想数值。又因为我们可以随意调整减去的序列内容,所以可以让根加上的少一些,得到正确答案。
例2
这次仅将例1中的4改成了1。我们发现,如果按例1的思路,在两条路径上分别加上1, 1和2, 2,两个孩子是满足了,但根却只有3。此时我们需要再进行一次操作,让根加上2,成为5。
分析
造成上面两个例子不同的原因是什么呢?不难发现,当孩子之和大于根时,我们能以孩子个数的操作次数解决问题。然而,当孩子之和小于根时,我们不能直接满足根的需求,还需要再对根单独进行一次处理。这就是对于这种情况得出的结论。
回到原题
现在让我们再加上最后一个条件:将最终结果的定值改成一个区间。题目问的是最少几次操作,所以我们只需要想办法在之前树的基础上让答案最小。应该怎么做呢? 在上一节中,我们已经得出了以下结论(请务必再看一遍):
- 当孩子之和大于等于根时,操作次数不变;
- 当孩子之和小于根时,操作次数加一。
所以,想要让操作次数尽可能小,我们就要尽可能满足第一种情况,让操作次数不变。即,我们要让孩子之和尽可能大,才有可能大于根。 下面就好办了。我们使用dfs,从叶子开始,让叶子先取到最大值(也就是右端点),然后逐层向上比较。如果当前根的孩子之和大于它本身范围内的任何一个值,即大于最小值(左端点),那么就能满足条件1;如果小于最小值,那么死马当活马医,反正操作次数要加1了,不如让当前根的值取最大,让再上面一层操作次数不变的可能性大一点。
AC代码展示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+10;
int t,n;
int fa[maxn];
int l[maxn],r[maxn];
vector <int> G[maxn];
int ans=0;
int dfs(int step,int now){
if(G[now].size()==0){
ans++;
return r[now];
}
int val=0;
for(auto nxt:G[now]){
val+=dfs(step+1,nxt);
}
if(l[now]<=val){
// cout<<"val["<<now<<"]="<<val<<endl;
return min(val,r[now]);
}else{
// cout<<"val["<<now<<"]="<<r[now]<<endl;
ans++;
return r[now];
}
}
signed main(){
cin>>t;
while(t--){
for(int i=0;i<maxn;i++){
G[i].clear();
}
ans=0;
cin>>n;
for(int i=2;i<=n;i++){
cin>>fa[i];
G[fa[i]].push_back(i);
}
for(int i=1;i<=n;i++){
cin>>l[i]>>r[i];
}
dfs(0,1);
cout<<ans<<endl;
}
return 0;
}
注意细节 需要开long long,否则会过不了第11个点。