P2024 [NOI2001] 食物链 题解
题目描述
动物王国中有三类动物 $A,B,C$,这三类动物的食物链构成了有趣的环形。$A$ 吃 $B$,$B$ 吃 $C$,$C$ 吃 $A$。
现有 $N$ 个动物,以 $1 \sim N$ 编号。每个动物都是 $A,B,C$ 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 $N$ 个动物所构成的食物链关系进行描述:
- 第一种说法是
1 X Y,表示 $X$ 和 $Y$ 是同类。 - 第二种说法是
2 X Y,表示 $X$ 吃 $Y$。
此人对 $N$ 个动物,用上述两种说法,一句接一句地说出 $K$ 句话,这 $K$ 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 $X$ 或 $Y$ 比 $N$ 大,就是假话;
- 当前的话表示 $X$ 吃 $X$,就是假话。
你的任务是根据给定的 $N$ 和 $K$ 句话,输出假话的总数。
思路
这道题显然是并查集,那么我们需要考虑的是如何在并查集中把同类/不同类表示出来。如果我们将同类的合并到一个并查集里,不同类的不在同一个并查集,那么我们就无法记录不同类之间的关系。如果将不同类合并到一个并查集中,同类的也合并到一个并查集中,其中在并查集里它们有一定的次序,就可以解决以上问题了。
具体过程
当指令给出 $X$ 吃 $Y$ 时,我们就把 $X$ 指向 $Y$ 。不难发现,如果这些关系形成了一棵树或一条链,也就是从下到上下面的吃上面的,就会构成一个循环:每差三个就是一个同类。
当给出两者是同类的关系时,说明我们需要将两者合并到一个并查集中。但是不能乱合并,我们也需要体现出其中的层次关系。只需要让这两个同类合并后深度差三即可。所以找到合适的位置再合并就行了。
附:圆锥、球体体积推导
圆锥
一个圆锥可以看作是一个直角三角形绕直角边旋转一周的结果。同样的,我们如果用柱体的眼光看待,它就是大小渐变的圆堆积而成的物体。这么一来,我们就可以使用积分求出它的体积了。
如图,我们可以把圆锥进行“切片”操作。
对于每一个圆的半径,我们可以用相似三角形求解。
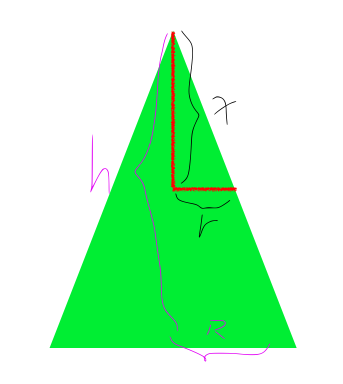
如图,我们假定圆锥的高度为 $h$ ,底面半径为 $R$ ,那么对于一个到顶点距离为 $x$ 的圆,它的半径 $r$ 就是 $R \times \frac{x}{h}$ 。对于 $x \in [0,h]$ ,我们将这些面积进行积分。
对于每一个圆的面积:
\[f(x)=\pi \times (\frac{R}{h} \times x)^2=\pi \times \frac{R^2}{h^2} \times x^2\]要求:
\[\int_{0}^{h} f(x)dx = F(h)-F(0)\]而:
\[F(x)=\pi \times \frac{R^2}{3h^2} \times x^3\]故最终的答案为:
\[F(h)-F(0)=\pi \times \frac{R^2}{3h^2} \times h^3=\frac{1}{3} \pi R^2 h\]球体
我们把上面的思路变换一下,将球体切片成大小不一的圆形。对于到圆心距离为 $x \in [-R,R]$ 的圆的面积可以表示为:
\[f(x)=\pi (\sqrt{R^2-x^2})^2=\pi R^2- \pi x^2\]积分一下:
\[F(x)=\pi R^2 x - \frac{\pi}{3}x^3\]求得体积:
\[\int_{-R}^{R}=F(R)-F(-R)=(\pi R^2 \times R - \frac{\pi}{3}R^3)\times 2=\frac{4}{3}\pi R^3\]