CSP初赛单选整理
-
设 A 和 B 是两个长为 n 的有序数组,现在需要将 A 和 B 合并成一个排好序的 数组,请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 ( )次比较。
A. $n^2$ B. $n log n$ C. $2n$ D. $2n-1$
至少要做 $2n-1$ 次比较。下面是示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
#include <iostream> #include <vector> int cnt = 0; std::vector<int> mergeSortedArrays(const std::vector<int>& A, const std::vector<int>& B) { std::vector<int> result; int i = 0; // Index for array A int j = 0; // Index for array B while (i < A.size() && j < B.size()) { cnt++; if (A[i] <= B[j]) { result.push_back(A[i]); i++; } else { result.push_back(B[j]); j++; } } // Append remaining elements from A (if any) while (i < A.size()) { result.push_back(A[i]); i++; } // Append remaining elements from B (if any) while (j < B.size()) { result.push_back(B[j]); j++; } return result; } int main() { std::vector<int> A = {1, 3}; std::vector<int> B = {2, 4}; std::vector<int> merged = mergeSortedArrays(A, B); std::cout << "Merged Array: "; for (int num : merged) { std::cout << num << " "; } std::cout << std::endl; int comparisons = A.size() + B.size() - 1; std::cout << "Number of Comparisons: " << cnt << std::endl; return 0; }
-
下面不属于贪心算法的是()
A. 单源最短路径中的Dijkstra算法
B. 最小生成树的Prim算法
C. 最小生成树的Kruskal算法
D. 计算每对顶点最短路径的Floyd-Warshall算法Disjsktra算法在松弛操作时用到了贪心的思想;Prim、Kruskal在生树时优先选择最小边;Floyd算法使用的是动态规划的操作。
-
一个深度为5(根节点深度为1)的完全3叉树,按前序遍历的顺序给节点从1开始编号,则第100号节点的父节点是第()号。
A. $95$
B. $96$
C. $97$
D. $98$- 前序遍历:根,左,右;
- 中序遍历:左,根,右;
- 后序遍历:左,右,根。
在三号节点下,一共有12个节点,故3号的兄弟节点为16号、29号。在二号节点下,一共有39个节点。故二号节点的兄弟节点为42号、82号。所以第100号节点在第二层的第三个节点下面。然后再多画几个节点,就能轻松得到答案为 C 了。
-
1) 设G是连通无向图,则称经过G的每条边一次并且仅一次的路径为欧拉通路; 2) 如果欧拉通路是回路(起点和终点是同一个顶点),则称此回路为欧拉回路(Euler circuit)。
-
共有 $8$ 人选修了程序设计课程,期末大作业要求由 $2$ 人组成的团队完成。假设不区分每个团队内 $2$ 人的角色和作用,请问共有多少种可能的组队方案。( )
A. $28$ B. $32$ C. $56$ D. $64$
题目有歧义,直接 $C_8^2$ 即可。
-
以下四种编程语言中,属于弱类型编程语言的是:
A. Java B. Go C. Rust D. C++
- 强类型:Java、C#、Python、Ruby、Erlang、GO、Rust……
- 弱类型:C、C++、Javascript、Perl、PHP、VB……
强类型语言是一种强制类型定义的语言,即一旦某一个变量被定义类型,如果不经强制转换,那么它永远就是该数据类型。而弱类型语言是一种弱类型定义的语言,某一个变量被定义类型,该变量可以根据环境变化自动进行转换,不需要经过现行强制转换。
-
竞赛图也叫有向完全图。每对顶点之间都有一条边相连的有向图称为竞赛图。5 个点 的无标号竞赛图数是:( )。
A. $9$ B. $10$ C. $11$ D. $12$
答案为 D 。强联通,且大小为i的竞赛图个数为 $f_i=h_i-\Sigma_{j=1}^{i-1}h_j \times (j^i) \times f{i-j}$ 。
- 以下代码的输出结果是?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
#include <iostream> union U { bool flag1, flag2, flag3, flag4, flag5; signed short a; unsigned short b; enum E { CardA = 0, CardB = 1, CardC = 2, CardD = 142857 } e; } u; int main() { std::cout << sizeof(u) << std::endl; return 0; }
在这段C++代码中,定义了一个联合(union)类型
U,该联合包含了不同类型的成员变量,包括布尔型、有符号短整数、无符号短整数和枚举类型。联合类型允许在相同的内存位置存储不同类型的数据,但每次只能使用其中一个成员。计算
sizeof(u)将返回u这个联合类型的大小,即它所占用的内存字节数。在计算sizeof时,通常使用联合中最大成员的大小作为整个联合的大小。在这个联合中,枚举类型
E的最大值是CardD,它是一个较大的整数,可能需要占用较多的内存。因此,整个联合U的大小将由CardD的大小决定。通常,int类型占用4个字节,所以CardD的值为142857,占用4个字节。因此,
sizeof(u)的输出结果应该是4,即联合U占用4个字节的内存空间。输出结果是:
1
4
-
五个本质不同的店在没有重边或者自环的情况下,组成不同的无向图的个数是()?
五个不同的点,最多可有 $4+3+2+1=10$ 条边。每条边有或没有,所以最终结果为 $2^{10}=1024$ 。
-
以下代码的输出结果为?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
#include <iostream> using namespace std; int ans=0; void dfs(int x){ ++ans; if(x<=1) return; dfs(x/3); if(x/3+1<x) dfs(x/3+1); if(x/3+2<x) dfs(x/3+2); } int main(){ dfs(10); cout<<ans<<endl; return 0; }
-
中国计算机学会成立于()年?1962年。
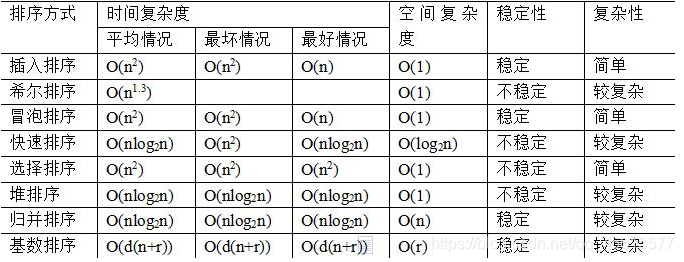
- 各种排序的比较: